Fundamentos | Coeficientes de Reducción |
Representación de la Circunferencia |
COEFICIENTES
DE REDUCCIÓN
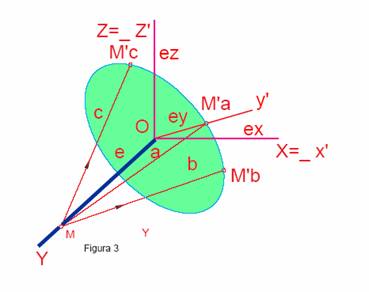
Supongamos que OM
es igual a la unidad e y proyectamos en la dirección a, la
dirección OM’a = ey, es la escala axonométrico ey sobre el eje Y.
Se llama coeficiente de
reducción del eje Y a la relación que existe entre la
media real y la reducida. Figura 3.
|
Cy = OM'a / OM = ey/e |
Siendo ey la medida
reducida e y la real.
Como ex y ez
están en verdadera magnitud, sus escalas y coeficientes de reducción ex = ez = e. De proyectar el punto M en direcciones a, b,
c, de tal forma que forme el mismo ángulo con el cuadro, sus
proyecciones M’a, M’b, M’c, equidistan de O, conservándose
constante la escala y el coeficiente de reducción.
|
ey = OM'a / OM = OM'b/ OM = OM'c /OM |
Ya que OM’a = OM’b = OM’c. Por tanto para un mismo valor del
coeficiente de reducción le corresponden infinitas direcciones de proyección (generatrices
de un cono de revolución) de vértice M
y eje OM. Figura 3.
Para que la perspectiva quede
definida es necesario fijar la posición del eje Y’ y su coeficiente de
reducción. La primera determina el plano proyectante de Y, y la segunda, la
inclinación de la dirección de proyección respecto al cuadro.
DEFINICIONES Y
NOMENCLATURA.
La posición del eje Y
viene dada por el ángulo que forma con X, si el eje es la
bisectriz de los ejes XZ, formará con X, 135º, en este caso la
perspectiva se llama regular. Los ángulos más utilizados en la práctica son: 30º,
15º, 45º y 60º.
El coeficiente de
reducción se suele tomar menor que la unidad. En caso contrario, las figuras
aparecerán alargadas en el sentido de Y. Los coeficientes de reducción más
utilizados son. 1/2, 2/3 Y 3/4.
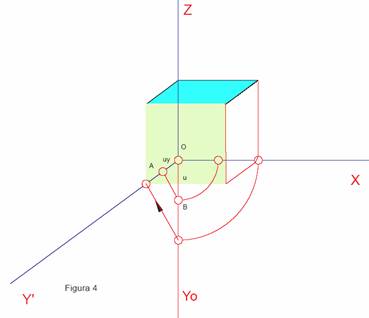
El coeficiente de reducción se
expresa gráficamente señalando sobre Y’ la magnitud OA’= ey,
y sobre la prolongación de Z el segmento O(A) = e.
- Resolución mínima 800x600