1.6. COEFICIENTES DE REDUCCIÓN

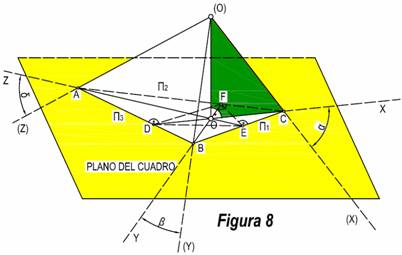
Al proyectar una figura sobre el plano del cuadro, esta será ligeramente más pequeña. Esta diferencia estará en función del ángulo que forme el plano del cuadro con los ejes del sistema,  (α_, β, γ), (figura 8). Este valor será el coeficiente de reducción del sistema.

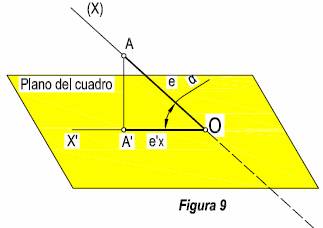
            Para estudiar estos coeficientes con mayor simplicidad, consideremos un eje del sistema por separado.   (Figura 9). El ángulo que forma en este caso el eje (X), y su proyección sobre el cuadro le llamamos α,  al eje en el espacio le designamos por (X), y su proyección sobre el cuadro por X.

            En la figura, se verifica que:

A’O = AO  cos α, en donde,

AO  es igual a la verdadera magnitud a proyectar. A’ O es la proyección sobre el plano del cuadro de la magnitud AO y

cos α , es el coeficiente de reducción ( ángulo que forma el eje con el plano del cuadro). Tendremos pues, tres coeficientes de reducción, cuyos valores serán cos α, cos β y cos δ.

            Por tanto cualquier magnitud e tomada sobre el eje X, nos dará al proyectarse sobre el plano del cuadro, el valor  ex, la relación entre ambos valores es lo que se conoce como coeficiente de reducción para el eje X, al cual le designaremos por Cx. Aplicando el mismo razonamiento para los tres ejes tendremos:

,  

Por tanto en el sistema axonométrico existirán tres coeficientes de reducción, uno por cada eje del sistema.