1.5. TRIANGULO DE TRAZAS.

Es la intersección del plano de proyección con las tres caras del triedro. Vamos a demostrar lo siguiente:

Ø                 Si trazamos distintos planos de proyección, los triángulos de trazas serán semejantes.

Ø                 Una proyección no depende del triangulo de trazas, si no, de la posición que ocupa el plano del cuadro.

Ø                 La alturas de un triángulo de trazas son los ejes del sistema.

Ø                 El triangulo de trazas será siempre acutángulo.

Ø                 Las bisectrices del triangulo órtico serán los ejes del sistema.

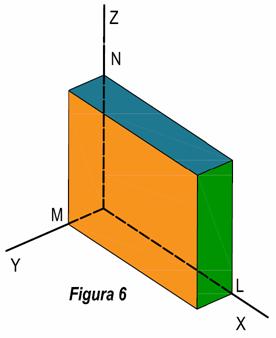
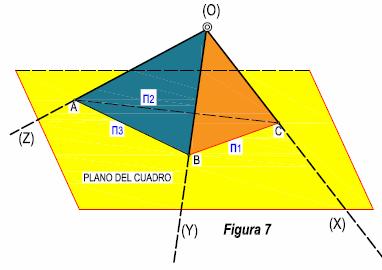
Consideremos un triedro trirrectángulo con el vértice hacia arriba, y lo cortamos por un plano paralelo al cuadro, Figura 7.  Los segmentos  AB = π_3,  AC = π₂   y    BC = π_1,  serán las trazas, intersección del triedro con un plano paralelo al cuadro. Si repetimos esta operación con otro plano cualquiera paralelo al cuadro, observaremos que los triángulos de trazas serán semejantes.

De acuerdo con lo anterior, el triángulo de trazas estará determinado por la posición que ocupe del plano de proyección con respecto al triedro. Por tanto la proyección no depende del triángulo de trazas.

 Consideremos el plano paralelo al cuadro como plano de proyección, y proyectemos ortogonalmente, tendremos que los puntos A, B, C, intersección de las trazas del cuadro con los ejes se proyectan sobre si mimo, ( puntos dobles), y el vértice (O), se proyecta en O, perpendicular trazada al plano del cuadro. Las rectas que unen O con A, B, C, serán las proyecciones de los ejes (X), (Y) (Z), sobre el plano de proyección, que le denominaremos, X, Y, Z.

De acuerdo con el teorema de las tres perpendiculares, que dice “ si dos rectas en el espacio (Z) y _, π₁  son perpendiculares en el espacio y una de ellas π_1, es paralela a un plano ( plano de proyección), sobre el cual se proyecta el conjunto ortogonalmente, se obtienen dos rectas Z y π_1, que son perpendiculares entre si. ( hemos considerado que π₁  se proyecta sobre si mismo). Igualmente aplicaríamos los ejes X, Y.

Por tanto podemos enunciar que los ejes de un sistema axonométrico, son las alturas del triángulo de trazas y serán perpendiculares a los lados de dicho triángulo.