1.2. ELEMENTOS QUE INTERVIENEN EN EL SISTEMA

Imaginemos la esquina de la clase y que esta la apoyamos en la pizarra por el vértice O, (figura 1), de tal forma que las aristas donde concurre el suelo y las dos paredes, quedan situadas en posición oblicua a la pizarra. La pizarra puede ser el plano del dibujo, llamada también plano del cuadro o plano proyectante.

El suelo y las dos paredes serán los planos proyectantes. Por tanto cuatro serán los planos que intervienen en el sistema, tres planos formado un triedro trirrectángulo y un cuarto plano que es el plano del dibujo. La única condición que deben cumplir estos planos es, que el plano del dibujo o cuadro no puede ser paralelo a ninguna cara o estar contenida en la misma.

La intersección de dos caras forman una arista, a la que llamaremos ejes coordenados, y por tanto serán tres los ejes.

La recta intersección de lo planos verticales ( las paredes) con el suelo, nos determinará el eje X e Y, y la intersección de las dos paredes el eje Z. El punto donde concurren los tres ejes le llamaremos vértice y lo designaremos por (O).

Estos tres planos forman un triedro trirrectángulo, y cada una de las aristas es perpendicular a la cara que no la contiene.

Una vez definidos los elementos que inte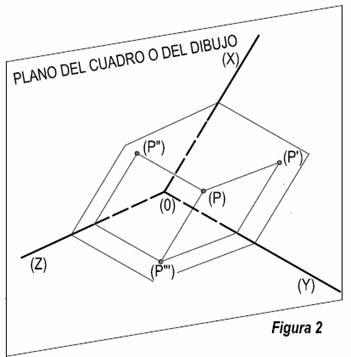rvienen, vamos a indicar el mecanismo de proyección.

Situemos un punto en el centro de la clase, nos imaginamos una línea que pasando por dicho punto sea perpendicular al suelo y paredes de la clase. El punto de intersección de dicha línea con los planos ( suelo, y paredes), tendremos tres proyecciones. Figura 2. De esta forma tendremos que, la proyección sobre el suelo la llamaremos horizontal, la situada en la pared derecha, vertical primera y la situada en la pared izquierda vertical segunda.

1.3.         CONVENIOS Y ANOTACIONES

Ahora tendremos que establecer unos convenios que sean admitidos internacionalmente y que nos permitan interpretar una proyección. Por tanto un punto en el espacio será representado por una letra mayúscula encerrada entre paréntesis, y que sus proyecciones se representarán por la misma letra acompañada de una, dos o tres comillas, según sea la proyección, horizontal, vertical primera o vertical segunda respectivamente. Entendiendo que estas proyecciones se encuentran situadas en el espacio. (Figura 2).