1.4. FUNDAMENTOS DEL SISTEMA.

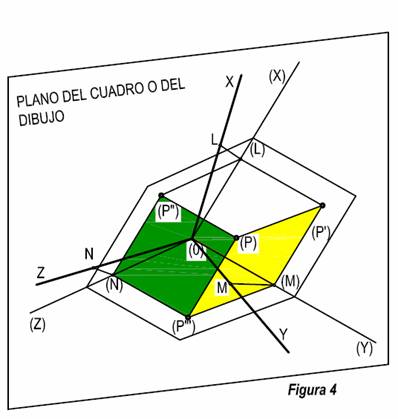
Partimos de un punto en el espacio (P). (Figura 3 y 4). El primer paso es, proyectar sobre el plano del cuadro los ejes (X), (Y), (Z), (aristas del cubo formado por las paredes de la clase), de tal forma que el punto (L), se proyecte en L, el (M), en M, y el (N) en N. El punto (O), vértice del triedro que se encuentra apoyado en el plano del cuadro, se proyectará sobre si mismo en O. Uniendo el punto O con los puntos anteriores, tendremos los ejes en proyección X, Y, Z. (Figura 4).

Tendremos que considerar que al proyectar sobre el cubo que forman las paredes de la clase, las proyecciones del punto ( P ), ( P’), ( P”) y ( P”’) , se encuentran en el espacio, y por tanto, en tres dimensiones.

Seguidamente pasamos a proyectar todo el conjunto sobre el plano del cuadro, de forma perpendicular, así tendremos que los puntos anteriores, se proyectan en P, P’, P” y P”’. (Figura 5).

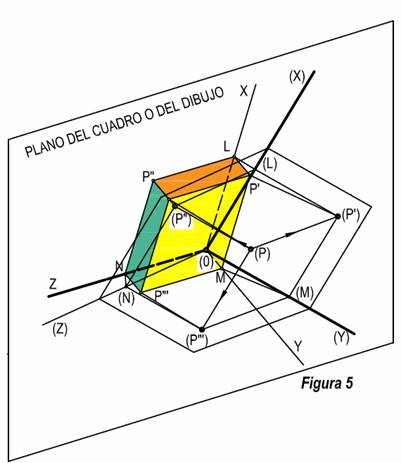De acuerdo con lo anterior, un punto tendrá cuatro proyecciones, una proyección directa P, que es la que se entiende por perspectiva del cuerpo en el espacio sobre el plano del cuadro, y otras tres que le llamaremos proyecciones previas o proyecciones de proyecciones. Estas proyecciones se encuentran sobre el plano del cuadro.

Como puede observarse en la figura 6, una vez girados los ejes hasta ocupar la posición con la habitualmente trabajamos, la recta PP’, es paralela al eje Z, la PP”, al eje Y, y la PP”, al eje X, tanto en el espacio como en proyección.