1.8. TEOREMA DE SCHLÖMILCH- WAISBASCH

Enunciamos este teorema en dos partes, sin entrar demasiado a fondo.

a)      las proyecciones ortogonales de los ejes del triángulo sobre el plano cuadro, son las bisectrices del triángulo órtico.

b)     Los cuadrados de las escalas axonométricas y la natural e. son respectivamente proporcionales a los lados y semiperímetro del triángulo órtico del de referencia.

e_x²/ a = e_y²/b = e_z²/c = e²/p

siendo a, b, c, los lados del triángulo órtico, y p, el semiperímetro.

Si se cumple que dicho triángulo órtico es equilátero ( caso del sistema isométrico), tendremos:

a + b + c =  P = 2p de donde:

                       (e_x²  + e_y² + e_z² ) / (a + b + c) = e² /p

                       e_x²  + e_y² + e_z² =2e, o lo que es igual

Si se trata del sistema isométrico, los ángulos que forman los ejes con el plano del cuadro son iguales, por lo que se cumplirá:

<

cos² α = cos² β = cos² λ =  cos² γ    de donde

cos² α + cos² β + cos² λ = 3 cos² γ = 2e    de donde

cos γ  =

Coeficiente de reducción en el sistema isométrico, como se verá más adelante.

1.9.         RELACIONES ENTRE EL TRIÁNGULO DE TRAZAS, LOS COEFICIENTES DE REDUCCIÓN Y LAS ESCALAS AXONOMÉTRICAS.

Conociendo una cualquiera de las relaciones anteriores quedan determinadas las otras dos. Para una mayor claridad resolvamos algunos ejercicios.

Ejercicio 1.-Dado un triángulo de trazas determinar.

a)                             La dirección de los ejes coordenados, proyectados sobre el cuadro.

b)                             Determinar los ángulos que forman los ejes con el plano del cuadro. ( coeficientes de reducción)

c)                             Hallar las escalas de reducción y la natural, en cada uno de los ejes, y construir la escala volante.

Para resolver la primera parte del ejercicio, tendremos que aplicar la propiedad que dice “ las proyecciones de los ejes coordenados coinciden con las alturas del triángulo de trazas”, por tanto por cada uno de los vértices del triángulo de trazas P, Q, R, trazamos perpendiculares al lado opuesto, quedando definidos los ejes. (Figura 10).

            Para determinar la segunda parte del 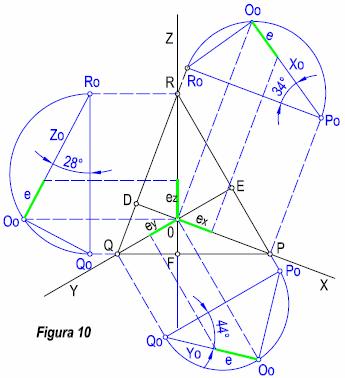ejercicio, se secciona el triedro por un plano proyectante que pase por cada uno de los ejes, y a continuación se abate la sección producida. Esta sección abatida nos dará el verdadero valor del ángulo de cada eje con los planos de proyección.

            Para hallar la escala de reducción, e_x se sitúa en la recta PR el valor real ( escala natural) y se trazan paralelas hasta que corte a la recta AD, el segmento e_{x ,} será el buscado. De la misma forma se actúa para el resto de los ejes.

Seguidamente pasamos a hallar el valor de las escalas métricas, que nos servirán para la construcción de una escala volante.

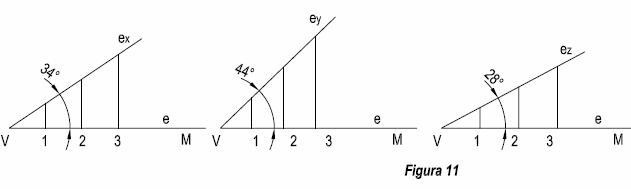
            Tengamos el segmento VM, dividido en cm. de la escala natural, tomando como vértice el punto V, se construyen los ángulos hallados anteriormente α = 34º, β = 44º, λ = 28º, y en la disposición indicada en la figura 11. Llevamos sobre el lado ex, ey, ez, divisiones de 10 mm. Por cada una de ellas, se trazan perpendiculares a los lados e de los ángulos construidos, que nos determina la escalas métricas correspondientes.

Ejercicio 2.- Dados los ángulos α = 30º, λ=38º, determinar los ejes axonométricos.

Trazamos una recta vertical que nos determina la dirección del eje Z, haciendo centro en un punto cualquiera (G), se traza una semicircunferencia, con un radio cualquiera. Por el punto N, trazamos una recta perpendicular, seguidamente por el extremo M, se traza una recta que forme un ángulo  λ con el eje Z, hasta que corte a la semicircunferencia en Oo, por donde se traza una perpendicular a MN, que nos determina el vértice del triedro. El ángulo O N Oo =  λ, será el que forme el plano XOY con el cuadro.

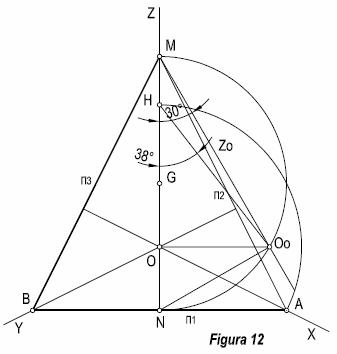
Por tanto la recta π₁, trazada por N, será la traza del plano XOY que buscamos. Por Oo, trazamos una recta que forme con el eje Z, el ángulo α= 30º dado, obteniendo el punto H. Con centro en O y radio OH, trazamos un arco que corte a π₁ en A; la recta OA, es la proyección del eje X, y por tanto AM, es la traza α₂ del plano con XOZ. La proyección del eje Y, pasa por O y es perpendicular a π₂, la traza π₃   pasa por B y es perpendicular al eje X.