1.    CILINDRO

 

1.1.        Se da un cilindro recto de revolución apoyado en el plano horizontal de proyección, definido por sus proyecciones vertical y horizontal. Se pide:

 

a) Determinar en proyección la sección producida por el plano oblicuo α.

 

b) Posteriormente determinar en verdadera magnitud los ejes de la elipse sección.

 

c) Por último construir a partir de dichos ejes  obtenidos anteriormente un Óvalo de cuatro centros. Figura 77.

 

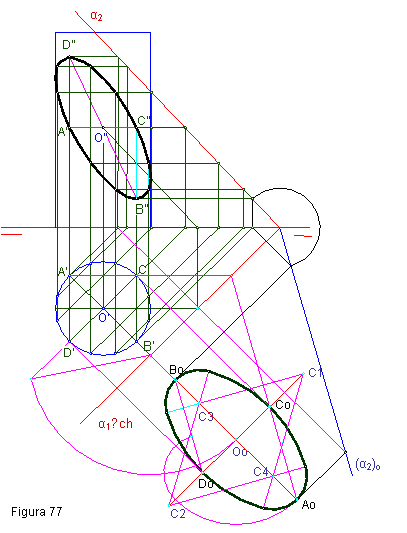1. Se divide la circunferencia un número de partes iguales, en nuestro caso 12. Solo se identifican las que definen los ejes. A’, B’, C’, D’,

 

2. Por medio de perpendiculares a la línea de tierra, hallamos las proyecciones segundas A”, B”, C”, D”

 

3. Por abatimiento y homotecia hallamos los ejes en verdadera magnitud, puntos A_o, B_o, C_o, D_o.

 

4. Por último construiremos la elipse de cuatro centros.

 

 

 

 

 

 

 

 

 

 

 

 

 

1.2.           Se da un cilindro oblicuo apoyado en el plano horizontal definido por sus proyecciones horizontal y vertical.

a)     Determinar en proyección y verdadera magnitud la sección producida por el plano α. Para resolver el problema se trabajará con 12 generatrices tomadas sobre la directriz del cilindro. Figura 78.

 

1. Dividimos la circunferencia en doce partes iguales, hallando unas generatrices que serán ficticias.

 

2. por tratarse de un plano proyectante, la traza α₂ cortara a las generatrices halladas. Puntos A”, B”, C”, D”.

 

3. Por medio de perpendiculares a la línea de tierra obtenemos las proyecciones A’, B’, C’, D’ y sus simétricos.

 

4. por abatimiento de la traza vertical α₂, obtendremos los puntos A_o, B_o, C_o, D_o. y su simétricos.