1.    PIRÁMIDE. REPRESENTACIÓN Y DESARROLLO.

 

La pirámide está generada por una recta, que sea poya en un punto fijo, llamado vértice, y se desplaza por  una superficie poligonal.

 

Si dicha superficie es un polígono regular y el vértice se sitúa en el centro geométrico del polígono, la pirámide será regular.

Si el polígono de la base es irregular o la altura de la pirámide no se sitúa en el centro del mismo, será irregular.

 

 

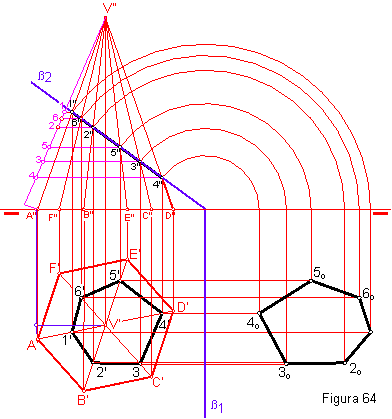
1.1.      Dada la pirámide recta  de base hexagonal apoyada en el plano horizontal. determinar:

 

1 La proyección vertical.

 

1o

2. La sección  producida por el plano β  en proyecciones y verdadera magnitud.

 

1. Partimos de un hexágono regular A’-B’-C’-D’-E’-F’, apoyado en el plano horizontal. Figura 64.

 

2. Hallaremos la proyección vertical de los puntos anteriores A’’-B’’-C’’-D’’-E’’-F’-, previamente determinaremos su centro V’ y el vértice V”.

 

3. Por ser un plano proyectante, su proyección vertical es una línea.

 

4. Una ver hallada la proyección vertical determinaremos la horizontal.

 

5. La verdadera magnitud de la sección se halla por abatimiento.

 

6. La determinación de la verdadera magnitud de la arista de halla por giro de la recta  V’- A’.

 

 

 

 

1.2.       Seccionar por el plano β₁-β₂, la pirámide de base cuadrangular, apoyada en el plano horizontal de proyección de la que se conoce la base y el vértice V’-V” se pide:

 

a)     Dibujar la proyección horizontal y vertical de la sección producida por dicho plano.

 

b)     Dibujar la verdadera forma de la sección.

 

c)     Realizar el desarrollo lateral de la transformada de la sección dando el punto V. figura 65.

1. Partimos del cuadrado de la base, A’-B’-C’-D’, apoyado en el plano horizontal de proyección. Hallamos sus proyecciones verticales A’’-B’’-C’’-D’’,  y el vértice V”.

 

 2. Por tratarse de un plano oblicuo, la traza del plano β₂ no corta a las aristas de la pirámide, sino que las cruza.

3. Por ello para hallar las intersecciones de las aristas de la pirámide con el plano β, tendremos que hacer contener a cada una de ellas en un plano proyectante, y hallar las intersecciones de ambos planos.

 

4. Hacemos pasar un plano proyectante por A’-C’, que determina el punto1”. El punto 3’, se encontrará en β_1. y 3”, en la línea de tierra.. El punto 1’ se obtiene trazando una perpendicular a la L.T.

 

4. El punto 2” y 4’, se puede hallar por homología.

 

5. Para obtener la verdadera forma de la sección, bastará con abatir las horizontales de plano que pasan por cada uno de los puntos 1’-2’-3’-4’.

 

6. Para hallar el desarrollo del a sección, tendremos que determinar la verdadera longitud de la arista de la pirámide, ya que esta es oblicua a los planos de proyección y por tanto no se encuentra en verdadera magnitud. Figura 66.

 

7. Eligiendo como eje de giro la recta que pasa por V’-V”, giraremos la recta B’-V’, hasta que esta ocupe la posición V’-B’₁, paralela a la línea de tierra. La recta 3-V”, será la verdadera magnitud de la arista del a pirámide.

 

El resto del a construcción puede deducirse de la figura 66.

 

 

 

1.3.      
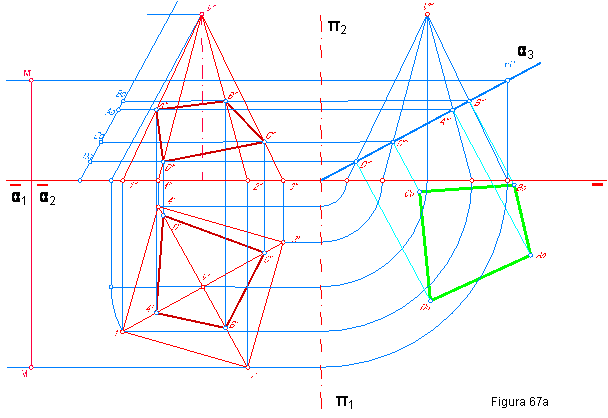
Dada la proyección horizontal de la pirámide recta regular de base 1’, 2’, 3’, 4’. apoyada en el horizontal: determinar

a)     En proyección y verdadera magnitud la sección producida por el plano α(α₁-α₂), que pasa por la línea de tierra).

 

b)     El desarrollo de la misma.

 

1. Se dibuja un plano cualquiera de perfil π (π_1- π₂)

 

2. Se halla la tercera proyección del plano α.

 

3. Se halla la proyección vertical de la pirámide

 

4,- Pasamos la pirámide a tercera proyección. La sección en tercera proyección vendrá determinada por la intersección del plano α con las aristas de la pirámide. Puntos A”’, B”’, C”’….

 

5. Hallamos la proyección segunda y primera de dichos puntos  A”, B”, C”… Y

A’, B’, C’…

 

6. La verdadera magnitud se halla trazando perpendiculares por los puntos A”’, B”’, C”’ D”’, y llevando sobre ellas la distancia de las segundas proyecciones al plano vertical tres.

 

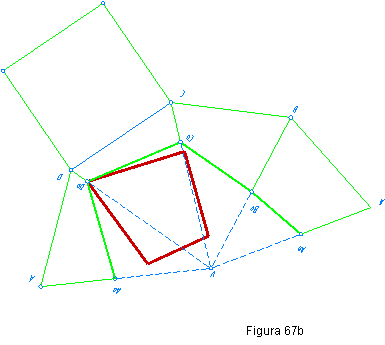
6. El desarrollo de la sección se realiza como en los ejercicios anteriores. Figura 67b.

 

 

 

1.4.         Hallar la proyección horizontal y vertical de la pirámide  hexagonal apoyada en el plano horizontal, teniendo en cuenta  que la arista 1’-V’ es una recta frontal.

 

a)     Por medio de cambio de plano, hallar la  proyección horizontal, vertical y verdadera magnitud de la sección producida por el plano α. Figura 68.

 

1.- Se halla la proyección V’ teniendo en cuenta que es una recta frontal.

 

2.- Se dibuja la proyección horizontal y  vertical  de la pirámide.

 

3.- Hacemos un cambio del plano vertical, de tal forma que este se convierta en proyectante trazando una nueva línea de tierra perpendicular a la traza horizontal de α₁.

 

4.- Hallamos la nueva proyección vertical de la pirámide.

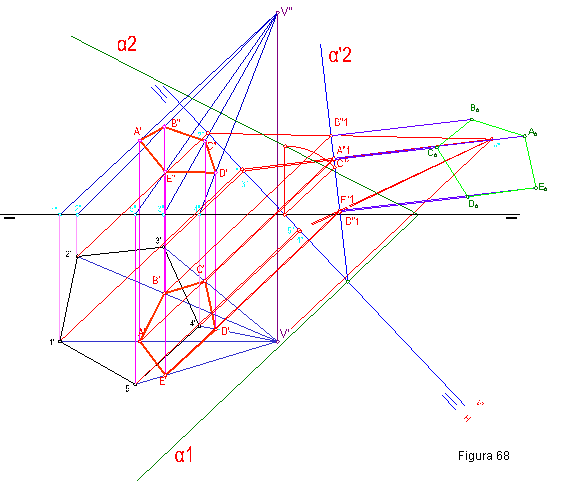
5.- La sección vendrá dada por la intersección  del α’₂ con las aristas de

la pirámide.  Puntos A”₁, B”₁, C”₁. Trazando perpendiculares a la nueva línea de tierra, hallamos los puntos A’, B’, C’. Seguidamente se halla la proyección vertical puntos A”, B”, C”.

 

6.- La verdadera magnitud se obtiene trazando por los puntos A”-1, B”-1, C”-1

y D”-1 perpendiculares a la traza vertical del plano y llevando sobre dichas rectas el valor del alejamiento de los puntos.

 

 

1.5.          Se da la verdadera magnitud de la base de una pirámide apoyada en el plano β( β1- β2).

 

a)     Hallar la proyección horizontal y vertical de la misma, sabiendo que su altura es 30 mm.

 

 

1. Hallamos la proyección horizontal y vertical de la base de la pirámide, obteniendo previamente la traza vertical del plano β2.

2.Trazamos una recta perpendicular a la trazas del plano β (β1-β2), que pase por O’-O”.

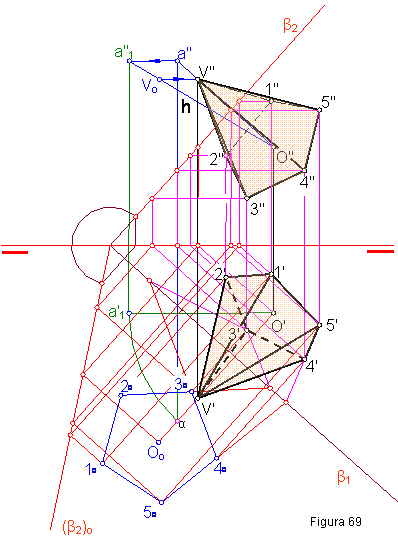
3. Elegimos un punto cualquiera de la recta anterior. a’-a”. Giramos dicha recta para obtener su verdadera magnitud.

 

4. Llevamos sobre dicha recta la altura h = 30 mm, de la pirámide, obteniendo el vértice Vo y seguidamente el V’.