1.    PRISMA.

 

1.1.        En la figura se define un prisma recto apoyado en el plano de proyección horizontal, mediante la proyección horizontal de se base y su   altura. Se pide:

 

a)     Las proyecciones horizontal y vertical del prisma.

b)     Determinar en proyección y verdadera magnitud la sección producida por el plano α. Figura 70.

 

1. Dibujamos el alzado del prima levantando perpendiculares por los puntos 1’, 2’,3’ ,4’ que nos determinan su segunda proyección. Las proyecciones  5”, 6”, 7” y 8”, coincidirán en planta con las anteriores

 

2. Por ser un prisma recto las proyección horizontal de la sección A’, B’, C’, D’, debe coincidir con los puntos anteriores.

 

3. Por medio de las horizontales de plano h y l se obtienen las proyecciones verticales A”, B”, C”, D”.

 

4. Para hallar la verdadera magnitud de la sección abatimos la traza vertical del plano.

 

1.2.          Se da un prisma oblicuo de base pentagonal apoyado en el plano horizontal de proyección.

 

a) Dibujar la proyección vertical del mismo.

 

b) Determinar en proyecciones y verdadera magnitud la  sección producidas por el plano oblicuo α. Figura 71.

 

1.- Para resolver el ejercicio deben de darnos la proyección horizontal del prisma y la inclinación de una de las aristas.

 

2.- El ejercicio se resolverá por cambio del plano vertical hasta convertirlo

en proyectante. Ejercicio resuelto anteriormente.

 

            3. Como puede observarse los puntos 3’ y 4’, se encuentran en las trazas del plano y por tanto sus proyecciones 3” y 4”,estarán en la línea de tierra.

 

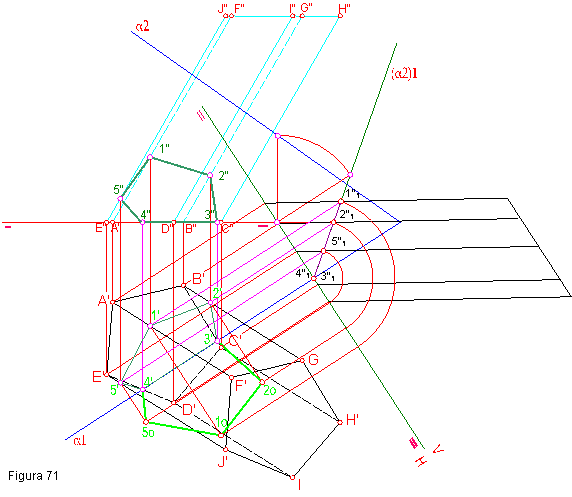
3.- La sección vendrá dada por los puntos 1”₁, 2”₁, 3”₁, 4”₁, 5”₁. que pasados a primera y segunda proyección tendremos las secciones buscadas.

 

 

 

1.3.          Dado un prisma de base pentagonal apoyado en el plano

Horizontal, se pide.

 

a) La proyección vertical del mismo.

 

b) Las proyecciones y verdadera magnitud las secciones producidas en el prisma por el plano β paralelo a la línea de tierra.

 

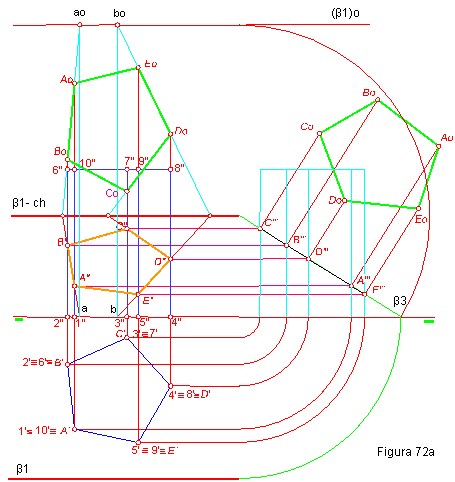
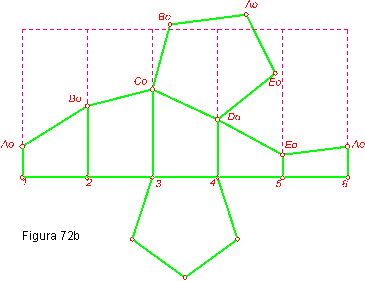
c) El desarrollo del prisma resultante como consecuencia de la intersección. Figura 72 a y b.

 

1.- Dibujamos el alzado del prisma, levantado perpendiculares por los puntos

1’, 2’,3’,4’,5’. A partir de las proyecciones verticales de estos puntos llevamos

la altura del prisma

 

2.- Una paralela a la línea de tierra determina los puntos 6”, 7”, 8”, 9” y 10”.

 

3.- Pasamos el prisma a tercera proyección y hallamos la intersección de este con β3 que nos determinan los puntos A”’, B”’, C”’, D”’, E”’. Hallando a continuación las proyecciones segundas. La proyección primera debe coincidir con los puntos 1’, 2’,3’,4’,5’, por ser las aristas perpendiculares al plano horizontal.

 

4.- La verdadera magnitud la hallaremos por dos procedimientos

 

 

1.4.         
Hallar la proyección horizontal y la vertical del prisma regular de base hexagonal apoyado en el plano oblicuo α. Figura 73.

1. En primer lugar colocamos la cara de apoyo en verdadera  magnitud, utilizando la traza α₁ como charnela. Hallamos las proyecciones horizontal y vertical, aplicando los procedimientos vistos; horizontales de plano, frontales, afinidad etc.
   

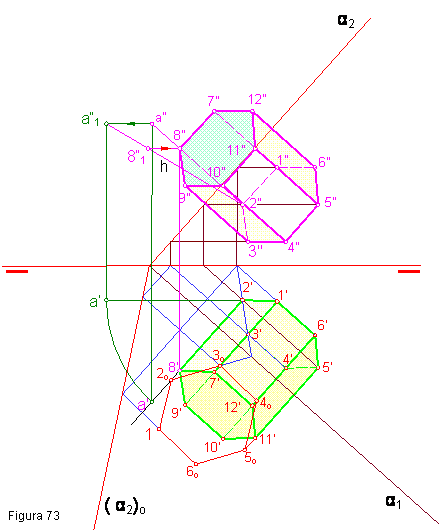
3. Por un punto cualquiera p.e. el 2’ trazamos una recta perpendicular a la traza del plano α₁.

 

4. Elegimos un punto cualquiera del a recta anterior a’- a”. y giramos el punto, a l aposición a’₁ y a”₁.

 

Sobre la recta 2”- a”₁, llevamos la altura del prisma. El resto del ejercicio es evidente.