1.    CONO

 

 

1.1.        Se da un cono equilátero recto de revolución apoyado por su base en el plano horizontal. Se pide:

 

         a)  La proyección Horizontal y vertical del cono.

 

b)  Determinar en proyecciones y verdadera magnitud las secciones interceptadas por los planos α y β. Figura 74.

 

1.- Se divide la circunferencia en doce partes iguales para obtener las generatrices ficticias del cono.

 

2.- Hallamos su proyección vertical.

 

3.- La sección vertical vendrá determina por la recta AG, y la horizontal por la proyección horizontal de los puntos correspondientes.

 

4.- Para hallar la proyección horizontal de los puntos JD, se hace pasar por ellos un plano π ₂  paralelo al horizontal y hallamos su proyección horizontal que será una circunferencia, esta nos determinan los puntos J’ y D’.

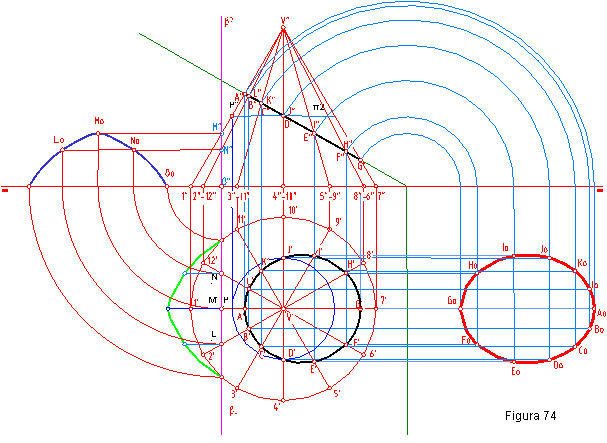
5.- Por último se halla la verdadera magnitud de la sección abatiendo el plano vertical α_2.

 

 

6. La intersección del plano de perfil β (β ₁ – β₂) viene dada por la intersección de las aristas ficticias con dicho plano. Puntos M”, N”, O”.

 

7.- También puede resolverse trazando perpendiculares por M’, N’,L’ a la traza

horizontal del plano y llevando sobre las mismas el valor de las cotas de dichos puntos.

 

 

 

1.2.          Dada una superficie cónica recta de revolución apoyada por su base en el plano horizontal de vértice V’-V”,. Se pide:

 

a) Representar la proyección horizontal y vertical.

 

a) Hallar las secciones en proyecciones y verdadera magnitud producidas por el plano α (α ₁ – α ₂) perpendicular al horizontal. Figura 75.

 

1.- Dividimos la base del cono en doce generatrices ficticias y hallamos la proyección vertical del mismo.

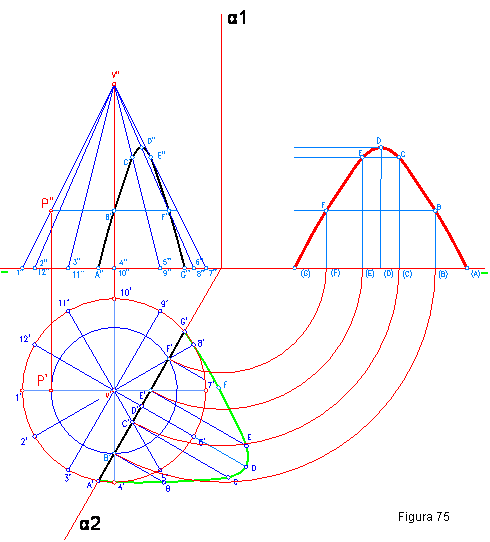
2.  Para hallar el punto B’ se traza una circunferencia con radio V’ B’. Explicado en el ejercicio anterior.

 

3.  La proyección horizontal vendrá dada por los puntos A’, B’, C’, D’ E’, F’, G’.

ya de que se  trata de un plano proyectante vertical  y las aristas ficticias cortarán a la traza horizontal.

 

4. levantando perpendiculares a la línea de tierra se obtendrán los puntos. A”, B”, C”, D”, E”, F”, G”. que determinan la sección vertical.

 

5.  La verdadera magnitud se halla levantando perpendiculares por los puntos A’, B’, C’, D’ E’, F’, G’. y llevando sobre ellas el valor de las cotas. También se puede hallar abatiendo el plano horizontal.

 

 

 

 

 

1.3.          Dada una superficie cónica recta de revolución apoyada por su

base en el plano horizontal de vértice V’-V”, Se pide:

 

a)     Representar la proyección horizontal y vertical.

 

b)    Hallar las secciones en proyecciones y verdadera magnitud producidas por el plano oblicuo α. Figura 76.

 

1.- Se divide la circunferencia en un número de partes iguales, por ejemplo ocho. Seguidamente se halla la proyección vertical.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

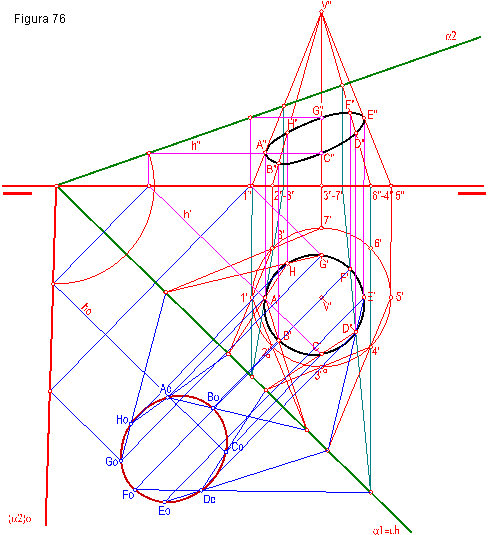
2. La intersección del plano con el cono se realizará por medio de intersección de aristas con el plano y por homología.

 

3. Para hallar la verdadera magnitud abatiremos el plano α₂. Se utilizará el procedimiento de homología y líneas horizontales de plano.