1.    ALFABETO DEL PLANO

 

            Un plano queda definido por:

a)     Dos rectas que se cortan, o paralelas,

b)     Tres puntos no alineados

c)      Una recta y un punto.

d)     Los casos anteriores se reducen a dos rectas incidentes.

 

 

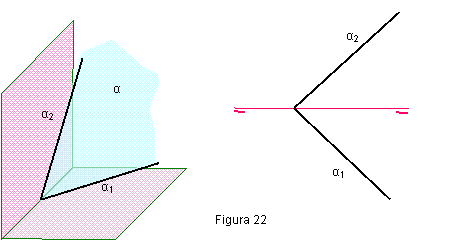
Un plano se representa por sus trazas.

 

Se llama trazas de un plano a la intersección de este con los planos de proyección.

 

Para su representación emplearemos letras griegas.

 

En la figura 21, se ha representado un plano oblicuo a los de proyección. A la traza vertical la hemos designado por  α₂  y  horizontal por del α_1.

 

1.1.          PLANO DE CANTO β, O PERPENDICULAR AL VERTICAL. PROYECTANTE VERTICAL.

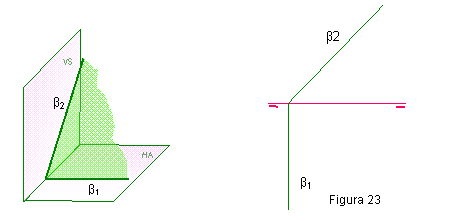La traza horizontal β₁ será perpendicular a la línea de tierra, y la vertical β₂  formará un ángulo con ella. Figura 23.

 

1.2.           PLANO HORIZONTAL  β, O PARALELO AL HORIZONTAL DE PROYECCIÓN PRIMER CUADRANTE.

                                                                      

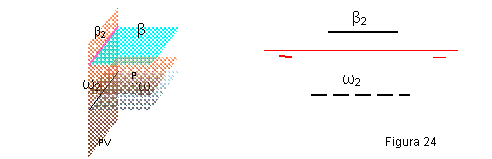Tendrá una sola traza, la vertical β₂, que será paralela a la línea de tierra, y estará por encima de ella.

.

Si el plano se encuentra en el cuarto cuadrante la traza será oculta ω₂. Figura 24.

1.3.           PLANO FRONTAL β PARALELO AL VERTICAL. Figura 25 a y b.

 

            Tendrá una sola traza que estará por debajo de la línea de tierra, y será paralela a la misma β_1.

 

Si el plano se encuentra en el segundo cuadrante  μ₁, será oculto y estará por encima de la línea de tierra.

 

 

 

 

 

 

 

 

 

 

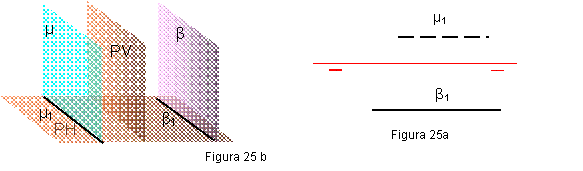
1.4.           PLANO DE PERFIL δ  O PERPENDICULAR A LA LÍNEA  DE TIERRA.

Sus trazas δ₁-δ₂ estarán en una misma perpendicular a la línea de tierra. Figura 26.

 

 

 

 

 

1.5.           PLANO  α PARALELO  A LA LÍNEA DE TIERRA.

Sus trazas  α₁-α₂ serán paralelas a la línea de tierra. Figura 27a y b.

 

            

 

1.6.          PLANO α  QUE PASA POR LA  LÍNEA DE TIERRA

 

                        Las trazas estarán confundidas con la línea de tierra. Para su definición será preciso representar un punto cualquiera del plano. Por ejemplo el punto

A(A’-A”). Figura 28 a y b.

 

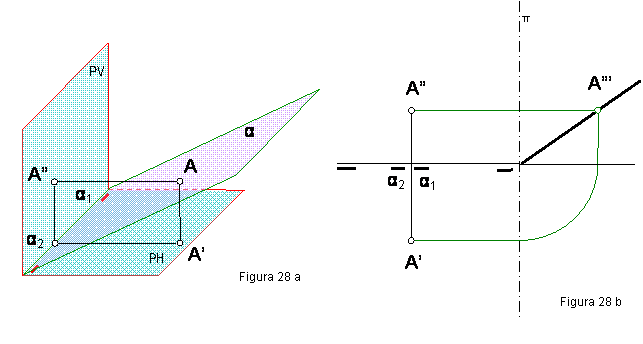
El plano α₁-α₂  se representará por las proyecciones del punto y dos pequeños trazos a cada lado de la recta que une los puntos.

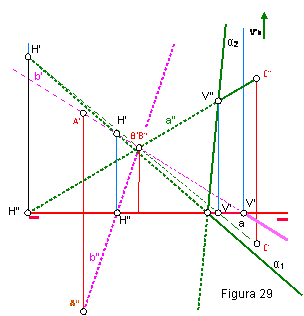
1.7.          DETERMINAR LAS TRAZAS DE UN PLANO DADO TRES PUNTOS DEL MISMO.

 Sean los puntos A, B y C dados por sus proyecciones

 

1. Utilizaremos el punto  B ( B’, B”) como punto común a ambas rectas.

2. Haremos pasar dos rectas a y b por dichos puntos.

 

3. Hallaremos las trazas de la recta a y b. Figura 29.

 

 

 

2.    SITUACIÓN DE RECTAS SOBRE PLANOS

 

Una recta pertenece  a un plano cuando las trazas homónimas de la recta se corresponden con las del plano.

 

            Por tanto, para situar una recta sobre un plano, bastará con que sus trazas se encuentren sobre las del mismo nombre del plano.

 

 

 

2.1.          SITUAR UNA RECTA OBLICUA m EN UN PLANO OBLICUO β₁.

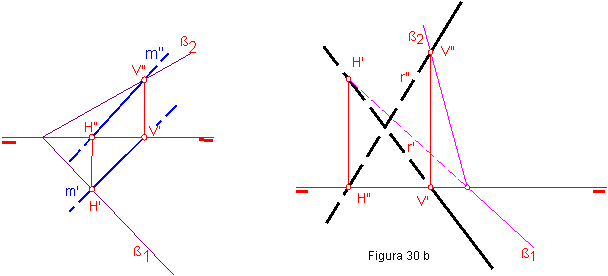Bastará con que las trazas de la recta  m (m’-m”) estén situadas sobre las homónimas del plano. Es decir  H’ debe estar en β₁ y V” en β₂.  Figura 30 a.

En la figura 30 b, se representa una recta oblicua r (r’-r”), en un plano oblicuo β (β₁-β₂), situada en el segundo cuadrante. Obsérvese que su trazas están por encima de la línea de tierra.

 

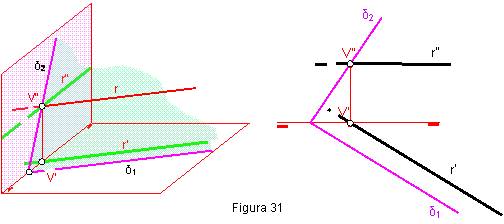
2.2.           SITUAR UNA RECTA  r  HORIZONTAL EN UN PLANO OBLICUO δ.

 

La traza horizontal de la recta será paralela a la horizontal del plano y la vertical será paralela a la línea de tierra. Esta recta recibe el nombre de recta horizontal de plano. Figura 31.

 

 

2.3.            SITUAR UNA RECTA FRONTAL p EN UN PLANO OBLICUO β.

 

            La traza vertical de la recta r “ será paralela a la traza vertical del plano β₂  y la horizontal β₁  será paralela a la línea de tierra. Figura 32.

 

 

 

 

 

 

 

 

 

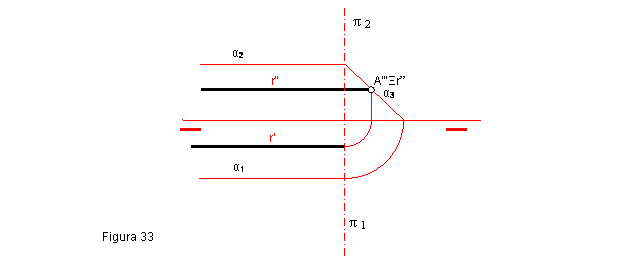
2.4.            DIBUJAR UNA RECTA r  PARALELA  A LA LÍNEA DE TIERRA EN UN PLANO  α PARALELO A LA LÍNEA DE TIERRA.

Para su representación, tendremos que dibujar la tercera proyección del plano α₃. Figura 33.

 

 

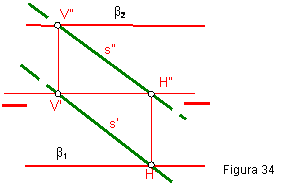
2.5.           SITUAR UNA RECTA   s OBLICUA EN  UN PLANO  β PARALELO A LA LÍNEA  DE TIERRA. Figura 34.

 

 

 

 

2.6.            SITUAR  UNA RECTA n DE
PERFIL EN UN PLANO α  PARALELO A LA LÍNEA DE TIERRA. Figura 35.